GENERATION DES TAS DE SABLE PAR TRONCATURES SUCCESSIVES DU TETRAEDRE

A partir d'une plaque polygonale à n côtés on génère une plaque à n + 1 côtés en coupant un coin.

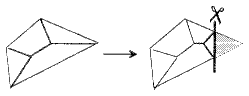
En partant du tétraèdre, quel que soit le coin coupé, on obtient la même configuration pour une base à 4 côtés. En continuant avec le quadrilatère, quel que soit le coin coupé, on obtient la même configuration pour une base à 5 côtés. Mais à partir d'une base pentagonale le résultat dépend du coin coupé.

On peut réaliser cette opération de troncature en agissant uniquement sur les formules. En effet, on part d'un tas de sable, ayant pour base un polygone à n côtés, et représenté par une formule (c1 ; c2 ; ... ; cn). On obtient un nouveau tas de sable, ayant pour base un polygone à n + 1 côtés en coupant le coin situé entre les faces i et j, qui ont respectivement ci et cj côtés. en partant de l'ancienne formule, on obtient une nouvelle fomule en :

1) insérant le chiffre 3 entre ci et cj

2)en augmentant ci et cj de 1.

Application pour passer d'une base hexagonale à une base heptagonale :

6 3 4 4 4 3 --> 7 3 4 4 4 4 3

6 3 4 4 4 3 --> 6 4 3 5 4 4 3

6 3 4 4 4 3 --> 6 3 5 3 5 4 3

5 4 3 5 4 3 --> 5 5 3 4 5 4 3

Les autres possibilités, ne font que donner, un des quatre tas déjà trouvés, sous forme d'un 7 uplet, éventuellement dans un ordre différent de celui de la formule.

Exemple : 5 3 5 3 5 3 --> 5 4 3 6 3 5 3 = 6 3 5 3 5 4 3

Cette méthode présente l'inconvénient majeur d'être récurrente.