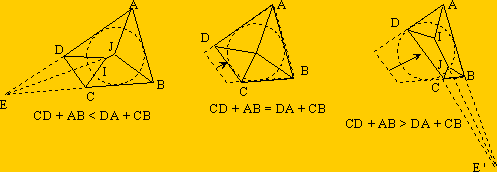Arête faîtière dans un quadrilatère :

Dans le cas général le tas a la forme d'un toit, et est constitué de deux triangles et de deux quadrilatères ayant une arête faîtière en commun.

L'arête faîtière est portée par l'intersection des faces de deux côés opposés.

Alors elle est sur la bissectrice formée par ces 2 côtés.

On part d'un quadrilatère que l'on va modifier en translatant un de ses côtés (ici CD).

Dans ce cas les angles restent constants.



Théorème de la pyramide :

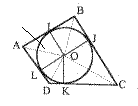
Un quadrilatère convexe admet un cercle inscrit ssi les sommes des longueurs des côtés opposés sont égales.

Un quadrilatère est articulé.

Ceci signifie que l'on peut modifier ses angles tout en conservant la longueur des côtés. En partant d'un quadrilatère vérifiant le théorème on forme de nouveaux quadrilatères qui génèrent eux aussi un tas pyramidal.

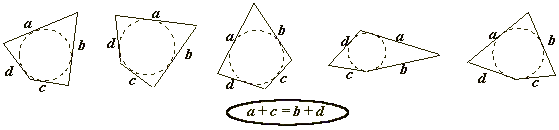
Evolution de la direction de l'arête faitière :

On voit que l'on passe, continûment de l'arête faîtière située sur la bissectrice issue de E, au cas de la pyramide (IJ=0) puis à l'arête faîtière situé sur la bissectrice issue de E'.

L'arête faîtière, quand elle existe, est portée par la bissectrice intérieure de l'angle formé par les côtés opposés du quadrilatère, dont la somme des longueurs est la plus grande.

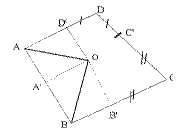
Cas où la base est un parallélogramme :

Quand la base est un parallélogramme alors l'arête faîtière a pour longueur la différence des longueurs des côtés de la base.


Démonstration de la pyramide :

Soit ABCD un quadrilatère admettant un cercle inscrit.
Et comme les bissectrices intérieures d’un quadrilatère convexe sont concourantes si et seulement si le quadrilatère admet un cercle inscrit,les bissectrices intérieures sont donc concourantes en un point O.
Soient I, J, K, L les projetés orthogonaux de O sur les côtés.
On a alors OI = OL et OÂI=OÂL, donc les triangles OAI et OAL sont égaux.
Donc LA=AI. On montre de même que IB=BJ, JC=CK et KD=DL.
Alors AB + DC = AI + IB + CK + KD = LA + BJ + JC + DL = DA + BC

Réciproquement,

Soit ABCD un quadrilatère convexe.
O est le point d’intersection des bissectrices intérieures de  et B. A’ (resp. B’ et D’) sont les projetés orthogonaux de O sur [AB] (resp. [BC] et [DA] )
On note a, b, c, d les angles de ABCD pris dans le sens direct. Les triangles OAD’ et OAA’ étant rectangles, les points A, A’, O, D’ sont cocycliques.
Donc ( OD’, OA’) = p - a De même (OA’,OB’) = p - b Alors (OD’,OB’) = -(a+b) [2p]
Soit C’ le point de [CD] tel que CC’= CB’. Alors on a DC’ = DD’.
En effet : DC’ = DC- CC’
= CB+AD-BA-CC’ (car AB+DC=BC+AD)
= CB’+BB’+AD’+DD’-BA’-AA’-CC’
= DD’ (car CB’ = CC’, BB’ = BA’, AD’=AA’ propriété des bissectrices)
Le triangle CC’B’ est isocèle donc (C’B’,C’C)=( p-c)/2 de même (C’C,C’D’) = (p-d)/2
Donc (C’D’,C’B’) = p-(p-d)/2-(p-c)/2=(d+c)/2 [2p]
Alors 2(C’D’,C’B’) = d+c =2p-(a+b) = (OA’ ,OB’) donc A’,B’,C’ et D’ sont cocycliques.
ABCD admet donc un cercle inscrit.

Démonstration des bissectrices :

Les bissectrices intérieures d’un quadrilatère convexe sont concourantes si et seulement si le quadrilatère admet un cercle inscrit.

Démonstration :

Soit ABCD la base, O le point d’intersection des bissectrices et I, J, K, L les projetés orthogonaux de O sur les côtés. Alors, OI=OJ=OK=OL et [OI] est perpendiculaire à [AB]. Respectivement pour [OJ], [OK], [OL] avec [BC], [CB], [DA]. (1)
Donc le cercle de centre O et de rayon [OI] est tangent aux cotés de ABCD.

Réciproquement, si O est le centre du cercle, alors (1) est vraie et O est sur chaque bissectrice.

Suite : Polygone à 2n côtés

Retour page precedente